10 Unsupervised Class Measurement

Topics: Unsupervised classification (clustering, latent class analysis).

Required reading:

• Chapter 13, Pragmatic Social Measurement

Further reading:

Theory

• Bartholomew et al. (2008), Ch 2 & 10
• Everitt and Hothorn (2011), Ch 6
• James et al. (2013), Ch 10.3
• Linzer & Lewis, “poLCA: An R Package for Polytomous Variable Latent Class Analysis”, Journal of Statistical Software, 42:10, 2011. https://www.jstatsoft.org/htaccess.php?volume=42&type=i&issue=10&paper=true
• Justin Grimmer and Gary King. “General purpose computer-assisted clustering and conceptualization” PNAS February 15, 2011 108 (7) 2643-2650
• John S Ahlquist and Christian Breunig. “Model-based Clustering and Typologies in the Social Sciences

---

10.1 Seminar

The data for this assignment are an extract from the US Bureau of Economic Analysis data on the distribution of employment by sector across all 51 US states (incl. Washington DC) in 2018. You can directly load the data file into R from the web with the following command:

load("week-10-bea-employment-by-state.Rdata")
bea <- 100*bea # convert proportions to percentages, for easier interpretation

It is recommended to multiply bea by 100 to convert everything to percentage points, as it makes the numbers easier to read at various points, but you can leave the values as proportions if you prefer.

For this assignment, you will also need to install and load the R package mclust:

# install.packages("mclust")
library(mclust)

# you may also need these packages
library(kableExtra)
library(magrittr)
library(ggplot2)
library(ggthemes)

1. What is the standard deviation of employment levels in each sector, across all US states? What do we learn from the relative magnitudes of these standard deviations?

kable(round(apply(bea,2,sd),2))

	x
Accommodation and food services	1.79
Administrative and support and waste management and remediation services	1.21
Arts, entertainment, and recreation	0.45
Construction	0.90
Educational services	1.15
Finance and insurance	1.42
Forestry, fishing, and related activities	0.45
Health care and social assistance	1.76
Information	0.48
Management of companies and enterprises	0.49
Manufacturing	2.88
Mining, quarrying, and oil and gas extraction	1.50
Other services (except government and government enterprises)	0.72
Professional, scientific, and technical services	2.09
Real estate and rental and leasing	0.81
Retail trade	1.26
Transportation and warehousing	0.98
Utilities	0.12
Wholesale trade	0.65
Government and government enterprises	3.31
Farm employment	1.35

The standard deviations describe the variation across states in employment in each sector. For example, the sector with the most variation across states is “Government and government enterprises”, with a standard deviation of 3.31 percentage points. This means that the percentage of employment in government varies a lot across states. In contrast, the sector with the least variation across states is “Utilities”, with a standard deviation of 0.12 percentage points. The level of employment (as a share of total state employment) in this area is very similar across different states. This is true in large part because very few people are employed in this sector, the mean is just 0.33 percent of total employment in a state.

2. If we are using unsupervised methods like principle components analysis or k-means clustering, what is the argument for doing our analysis on unstandardized levels of employment in each sector? What is the argument for doing analysis on standardized levels of employment in each sector, where the standardization is across states such that each sector has mean 0 and standard deviation 1?

The argument for using the unstandardised levels of employment is that these methods aim to “explain variation”, and so they will focus on identifying measures that predict the larger and more variable areas of employment. We might view these as more important, and therefore using the unstandardised indicators is what we want to do. Note that we can only defend this because all of the indicators are on the same scale: the percentage of total employment in the state.

The argument for using the standardised levels of employment is that even small economic sectors might indicate meaningfully different structures of the local economy. If we want to treat variation in all these sectors equally in identifying scales/clusters, we need to standardise in order to do that.

3. Use principle components analysis (see class assignment 8) on these data, using all indicators. Fit and save the principle components analysis with and without standardising the indicators. Plot the first (x-axis) and second (y-axis) principle components, with state name labels. Do two of these plots, one for PCA on standardised indicators and one for PCA on unstandardised indicators. You can create a new dataset with standardised indicators as below, but you can also make this choice using the argument scale.= of prcomp():

bea_standardised <- apply(bea,2,scale) # apply to all indicators

pcafit_unstandardized <- prcomp(bea,scale.=FALSE)

# either of the following will work...
pcafit_standardized <- prcomp(bea_standardised,scale.=FALSE)
pcafit_standardized <- prcomp(bea,scale.=TRUE)

# combine results
res <- data.frame(pc1_unst = pcafit_unstandardized$x[,1],
                  pc2_unst = pcafit_unstandardized$x[,2],
                  pc1_st = pcafit_standardized$x[,1],
                  pc2_st = pcafit_standardized$x[,2],
                  state = row.names(bea))

## base R
# par(mfrow=c(1,2))
# plot(pcafit_unstandardized$x[,1:2],
#      pch=16,col=rgb(0,0,0,0),
#      main="PCA on Unstandardized Indicators")
# text(pcafit_unstandardized$x[,1],pcafit_unstandardized$x[,2],
#      rownames(bea),col=rgb(0,0,0,0.5),cex=0.5)
# plot(pcafit_standardized$x[,1:2],
#      pch=16,col=rgb(0,0,0,0),
#      main="PCA on Standardized Indicators")
# text(pcafit_standardized$x[,1],pcafit_standardized$x[,2],
#      rownames(bea),col=rgb(0,0,0,0.5),cex=0.5)


## ggplot
# since the long state names are no fun (as in don't look good on the plot)
# let's try to replace the state names with the state codes. Two of the 
# datasets in-built to the package 'datasets' (which is pre-loaded in R)
# can be helpful here:

## first, combine codes and names into a dataset
us_codes <- data.frame("state"=state.name, "scode" = state.abb)

## merge with res (specifying `all=T` so that we keep DC)
res <- merge(res,us_codes, all=T)
res$scode <- ifelse(is.na(res$scode),"DC",res$scode)

p1 <- ggplot(res, aes(x = pc1_unst, y = pc2_unst, label = scode)) +
  geom_point() +
  geom_text(vjust=0.5,hjust=-0.2) +
  labs(x = "PC 1",y = "PC 2", title = "PCA on Unstandardized Indicators") +
  scale_x_continuous(breaks = seq(-5,20,5),limits = c(-7,20)) +
  scale_y_continuous(breaks = seq(-5,5,2)) +
  theme_clean() +
  theme(plot.background = element_rect(color=NA))

p2 <- ggplot(res, aes(x = pc1_st, y = pc2_st, label = scode)) +
  geom_point() +
  geom_text(vjust=0.5,hjust=-0.2) +
  labs(x = "PC 1",y = "PC 2", title = "PCA on Standardized Indicators") +
  scale_x_continuous(breaks = seq(-5,9,2),limits = c(-5,10)) +
  scale_y_continuous(breaks = seq(-2,8,2)) +
  theme_clean() +
  theme(plot.background = element_rect(color=NA))

ggpubr::ggarrange(p1,p2)

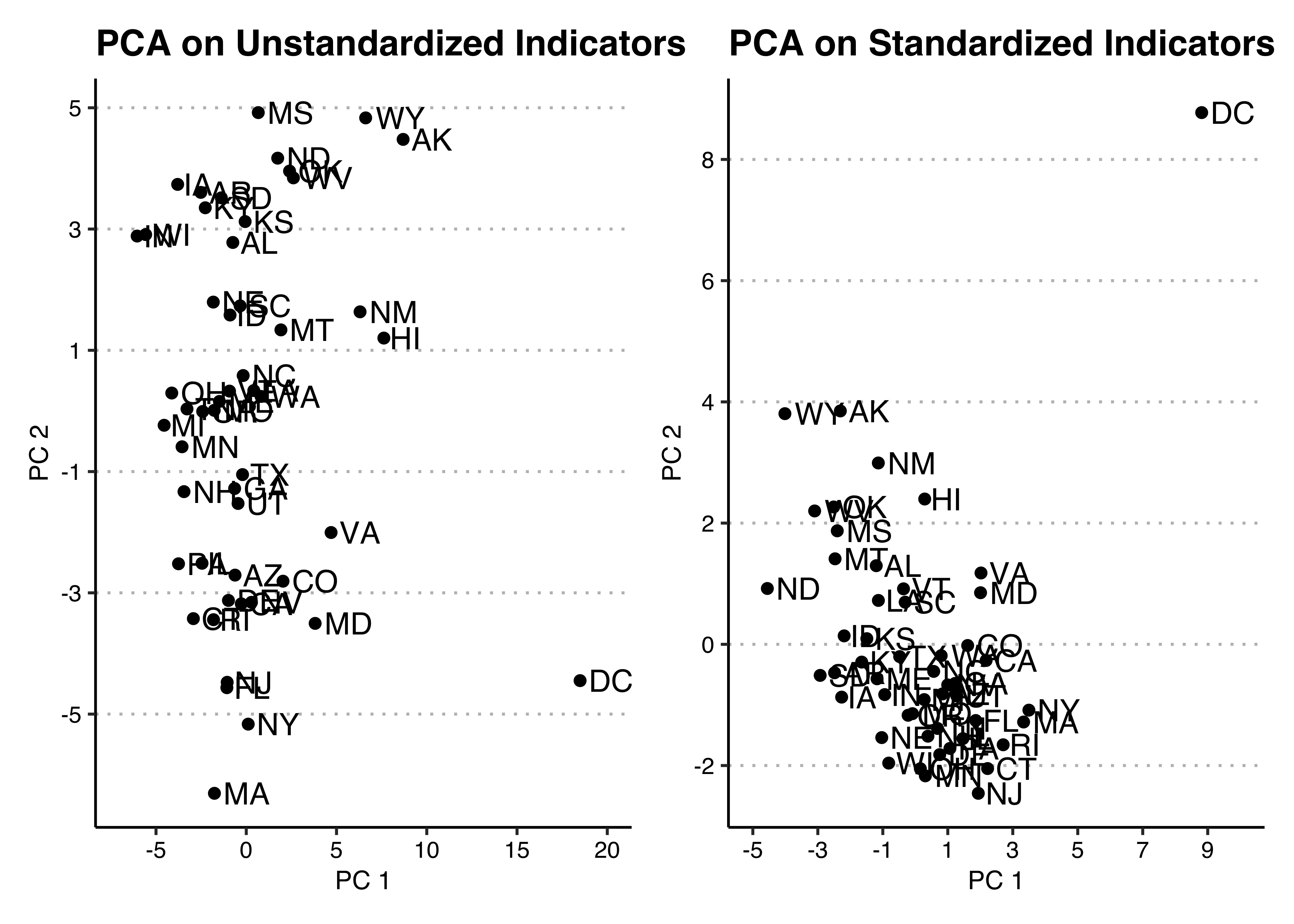
4. Investigate the obvious outlier that will be apparent in the PCA plots. Which indicators lead to this unit being an outlier? What (extremely basic) fact about American political geography explains why this unit is an outlier?

The District of Columbia (DC) is an outlier on PC1 in both analyses, and on both PC1 and PC2 in the analysis on standardized indicators.

One way to figure out which indicators are the reason for this is to standardise the indicators, and then look at the indicators in which the DC value is very positive or negative. Remember that a standardised variable is effectively a z-score, so any value outside of -2 to 2 is “extreme”.

knitr::kable( # function for making a nice, markdown format table to insert in this html document
round(
bea_standardised[grep("District of Columbia",rownames(bea)),] # print data for District of Columbia
,1)
)

	x
Accommodation and food services	0.2
Administrative and support and waste management and remediation services	-0.1
Arts, entertainment, and recreation	-0.5
Construction	-3.9
Educational services	3.8
Finance and insurance	-1.4
Forestry, fishing, and related activities	-1.2
Health care and social assistance	-1.6
Information	1.9
Management of companies and enterprises	-1.8
Manufacturing	-2.3
Mining, quarrying, and oil and gas extraction	-0.6
Other services (except government and government enterprises)	5.3
Professional, scientific, and technical services	4.5
Real estate and rental and leasing	-1.4
Retail trade	-5.6
Transportation and warehousing	-2.4
Utilities	-0.7
Wholesale trade	-3.6
Government and government enterprises	4.1
Farm employment	-1.3

As the output above indicates, the District of Columbia is an outlier on many of the indicators. It has an unusually high proportion of government jobs, professional scientific and technical services jobs, educational services jobs and “other services” jobs. In has an unusually low proportion of construction jobs, retail trade jobs and wholesale trade jobs. None of this is surprising, because unlike the other 50 units in the data, the District of Columbia is a single urban area rather than a mix of urban and rural areas, and is also the seat of the federal government.

5. Use k-means clustering on these data, using all indicators and \(k=5\) clusters. As with PCA, fit and save the k-means cluster analysis with and without standarising the indicators. Use the nstart = 50 option for kmeans() to ensure that you get a stable result (this will fit the algorithm 50 times from different start values, and select the best fitting one). Update your principle components plots, colouring by cluster.

set.seed(0013) # for stability of the cluster labels
kmeans_unstandardised <- kmeans(bea,5,nstart=50)
set.seed(0013) # for stability of the cluster labels
kmeans_standardised <- kmeans(bea_standardised,5,nstart=50)

# extract cluster assignments and add to our data
res$kclusters_unst <- as.factor(kmeans_unstandardised$cluster)
res$kclusters_st <- as.factor(kmeans_standardised$cluster)

# base R
# # this bit just makes the colours nicer than using default col = 1, 2, etc
# library(RColorBrewer)
# cols <- brewer.pal(n = 5, name = "Dark2")
# 
# par(mfrow=c(1,2))
# 
# plot(pcafit_unstandardized$x[,1:2],
#      pch=16,col=rgb(0,0,0,0),
#      main="PCA on Unstandardized Indicators")
# text(pcafit_unstandardized$x[,1],pcafit_unstandardized$x[,2],
#      rownames(bea),col=cols[kmeans_unstandardised$cluster],cex=0.5)
# 
# plot(pcafit_standardized$x[,1:2],
#      pch=16,col=rgb(0,0,0,0),
#      main="PCA on Standardized Indicators")
# text(pcafit_standardized$x[,1],pcafit_standardized$x[,2],
#      rownames(bea),col=cols[kmeans_unstandardised$cluster],cex=0.5)

# ggplot
p1<-ggplot(res, aes(x = pc1_unst, y = pc2_unst, 
                    label = scode, color = kclusters_unst)) +
  geom_point() +
  geom_text(vjust=0.5,hjust=-0.2) +
  labs(x = "PC 1",y = "PC 2", title = "PCA on Unstandardized Indicators") +
  scale_x_continuous(breaks = seq(-5,20,5),limits = c(-7,20)) +
  scale_y_continuous(breaks = seq(-5,5,2)) +
  scale_color_brewer("Cluster",palette = "Dark2") +
  theme_clean() +
  theme(plot.background = element_rect(color=NA),
        legend.position = "bottom")

p2 <- ggplot(res, aes(x = pc1_st, y = pc2_st, 
                      label = scode, color = kclusters_unst)) +
  geom_point() +
  geom_text(vjust=0.5,hjust=-0.2) +
  labs(x = "PC 1",y = "PC 2", title = "PCA on Standardized Indicators") +
  scale_x_continuous(breaks = seq(-5,9,2),limits = c(-5,10)) +
  scale_y_continuous(breaks = seq(-4,8,2)) +
   scale_color_brewer("Cluster",palette = "Dark2") +
  theme_clean() +
  theme(plot.background = element_rect(color=NA),
        legend.position = "bottom")

ggpubr::ggarrange(p1,p2)

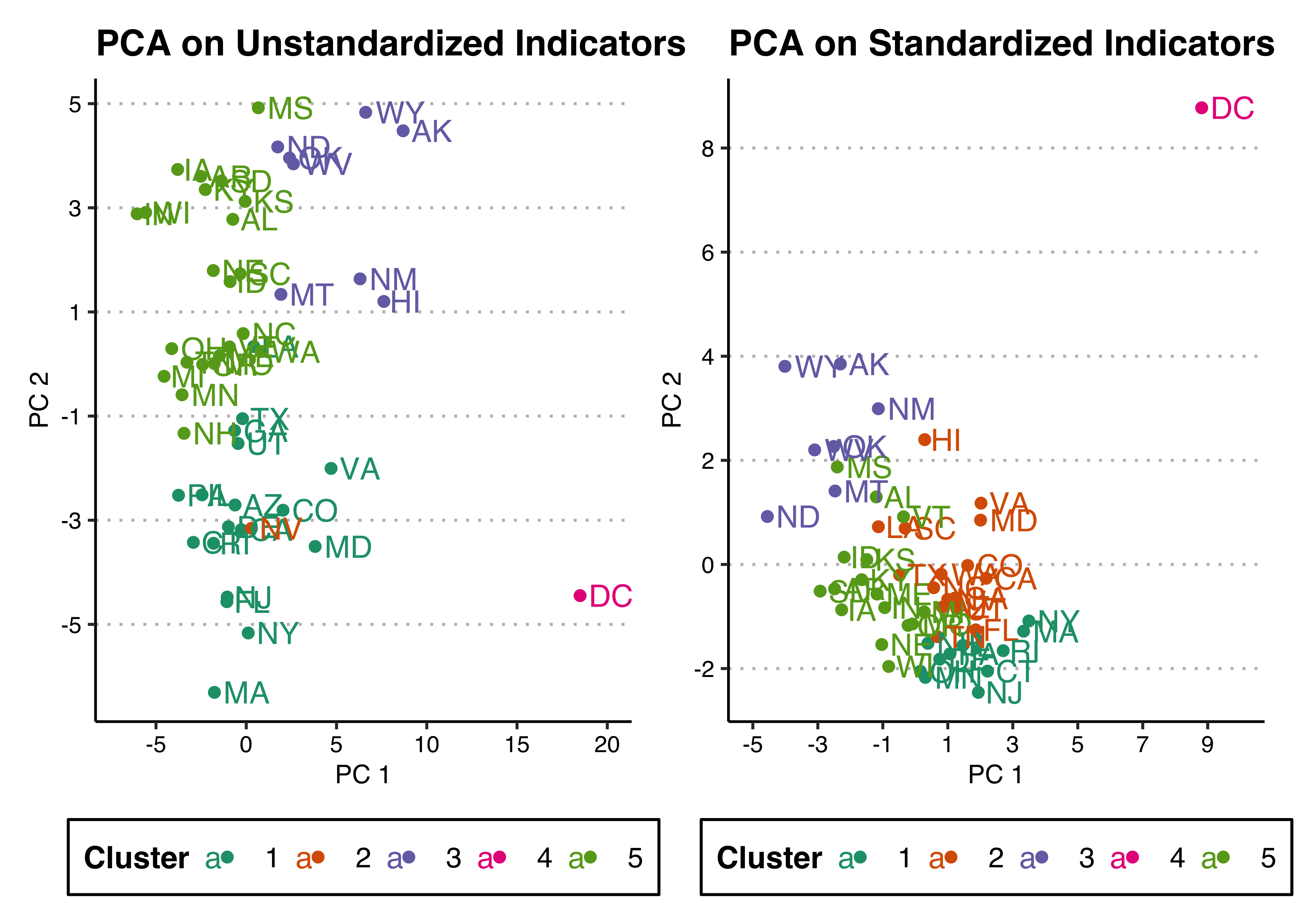
6. Describe the five clusters that you find using the unstandardised indicators. What distinguishes them from one another? You will need to explore a bit in the indicator data, and also look at the cluster means your_kmeans_object$centers. You might want to make a nice table of the latter, rounding the values appropriately for easy reading and comparison.

# Here are the centers of each cluster:
knitr::kable(  
  round(t(kmeans_unstandardised$centers),1), booktabs=T)

	1	2	3	4	5
Accommodation and food services	7.3	18.0	8.5	8.1	7.3
Administrative and support and waste management and remediation services	6.3	7.2	4.6	5.7	5.7
Arts, entertainment, and recreation	2.4	3.2	2.2	2.0	2.1
Construction	5.6	5.8	6.0	2.0	5.6
Educational services	2.8	1.0	1.4	6.7	2.1
Finance and insurance	5.9	4.7	3.7	2.9	4.6
Forestry, fishing, and related activities	0.3	0.1	0.9	0.0	0.7
Health care and social assistance	11.6	8.0	10.8	8.3	11.3
Information	1.7	1.2	1.2	2.4	1.4
Management of companies and enterprises	1.4	1.8	0.8	0.4	1.3
Manufacturing	5.5	3.4	4.0	0.2	9.3
Mining, quarrying, and oil and gas extraction	0.5	1.1	3.6	0.0	0.4
Other services (except government and government enterprises)	5.5	4.8	5.0	9.3	5.3
Professional, scientific, and technical services	7.7	5.5	5.1	15.8	5.6
Real estate and rental and leasing	5.1	5.8	4.4	3.4	4.1
Retail trade	9.5	9.8	10.2	2.9	10.4
Transportation and warehousing	4.6	6.4	4.0	1.9	4.0
Utilities	0.3	0.2	0.5	0.2	0.3
Wholesale trade	3.0	2.2	2.6	0.6	3.2
Government and government enterprises	12.0	9.5	17.6	27.1	13.0
Farm employment	0.8	0.3	2.9	0.0	2.3

7. As part of your investigations you could use the following code to map the clusters. Note that you need to assign your cluster assignments tocluster_assignments with something like cluster_assignments <- your_kmeans_object$cluster in order for this code to work.

library(ggplot2)
library(usmap)

cluster_assignments <- kmeans_unstandardised$cluster
classification_df <- data.frame(state=tolower(names(cluster_assignments)),
                                cluster=as.factor(cluster_assignments))

# And here is a US map of the assignments (DC is too small to see unless you zoom way in).
plot_usmap(regions="states", data=classification_df, values="cluster") + 
  labs(title="US States",
       subtitle="Clusters by Distribution of Employment Sectors.") + 
  scale_colour_brewer(palette = "Dark2") + 
  theme(panel.background = element_rect(color = "black",fill = "white"), 
        legend.position="right",
        legend.title = element_blank())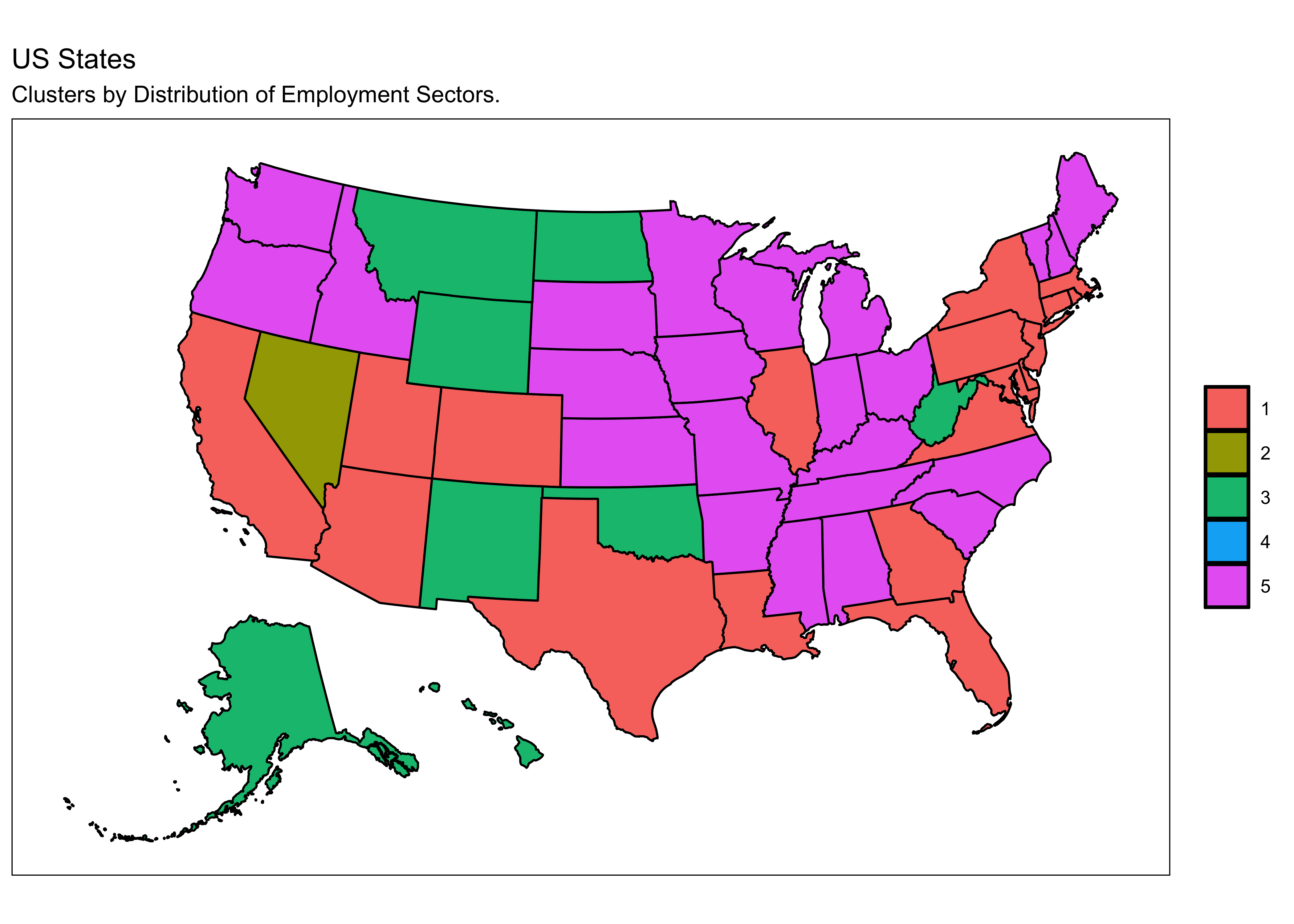 

There are two single state clusters. We already have seen why the District of Columbia is a single state cluster. The other single state cluster is Nevada. If we again look at the standardised indicators, we discover that Nevada is a massive outlier in “Accommodation and food services” and a moderate outlier in “Arts, entertainment, and recreation”.

knitr::kable(
round(
bea_standardised[grep("Nevada",rownames(bea)),]
,1)
)

	x
Accommodation and food services	5.7
Administrative and support and waste management and remediation services	1.2
Arts, entertainment, and recreation	2.1
Construction	0.3
Educational services	-1.2
Finance and insurance	-0.1
Forestry, fishing, and related activities	-1.0
Health care and social assistance	-1.8
Information	-0.6
Management of companies and enterprises	1.1
Manufacturing	-1.2
Mining, quarrying, and oil and gas extraction	0.1
Other services (except government and government enterprises)	-0.9
Professional, scientific, and technical services	-0.4
Real estate and rental and leasing	1.6
Retail trade	-0.1
Transportation and warehousing	2.2
Utilities	-0.7
Wholesale trade	-1.1
Government and government enterprises	-1.2
Farm employment	-1.1

Thus, the short answer for why Nevada is a single state cluster is Las Vegas. The major population center in the state is the only city in the US with an economy oriented around casino gambling, entertainment and hotels. Nevada, as a consequence, has a sufficiently weird distribution of employment relative to other states that the best way to explain variation in these data with five clusters is to give it a cluster of its own.

Thus, the remaining 49 states are divided among only 3 of the 5 clusters. Looking at the map above, if you think about where there are major cities in the US, you might notice that essentially all the states with major metropolitan areas are in cluster 1. You have to go down to the 15th largest metro area in the US before you find one that is in a state that is not in cluster 1 (Seattle). While some of the states in this cluster (Utah and Louisiana) do not have especially large cities in them, the cities are large relative to the state population. Most of the states with relatively high urbanization rates are in this cluster. If you examine the $centers of the clusters, you will see this cluster is relatively high in “Educational services”, “Finance and insurance”, “Health care and social assistance”, and “Professional, scientific, and technical services”.

This leaves two remaining clusters. For ease of examination, let’s look at the smaller of these, which is cluster 3. These turn out to be a bit of a grab bag of states, but they are distinctive because they have particularly high rates of “Mining, quarrying, and oil and gas extraction”, far more than any other cluster. The remaining cluster, cluster 5, has states with relatively high farm employment as well as manufacturing, but which lack substantial services industries like education and finance that are associated with major cities (cluster 1), highly developed accommodation and food services (NV, cluster 2), extensive resource extraction (cluster 3), or unusually high levels of government employment (DC, cluster 4).

8. Use the Mclust() function in the library(mclust) to fit Gaussian mixture models to the unstandardised data. Using the commands below, fit two 5-cluster models:
   1. One where all the clusters are assumed to have spherical, equal volume distributions of indicator values (EII), i.e where each indicator has the same standard deviation (spherical) and for all clusters (equal volume), and
   2. One where all the clusters are assumed to have diagonal, equal volume distributions of indicator values (EEI), ie.e where each indicator might have a different standard deviation (diagonal), but these are the same for all clusters (equal volume).

Have a look at the mean values of the first indicator for all five clusters for each of the models (EII and EEI), respectively. Also have a look at variance for the first and second indicators, respectively, as well as the covariance between them (you can access the variance-covariance matrix for equal shape models via your_mclust_model$parameters$variance$Sigma).

library(mclust)
mclust_fit_eii <- Mclust(bea,G=5,modelNames = "EII") # spherical, equal volume (and shape)
mclust_fit_eei <- Mclust(bea,G=5,modelNames = "EEI") # diagonal, equal volume and shape

round(mclust_fit_eii$parameters$mean[1,],3)
round(mclust_fit_eei$parameters$mean[1,],3)

## [1]  8.541  7.351  7.328  8.121 17.983
## [1]  7.968  7.161  6.962  8.121 17.983

The cluster means differ slightly between the two models, as they make different modelling assumptions, specifically: same variance across indicators and clusters vs same variance across clusters but different variance across indicators. They don’t differ at all in two of the clusters, which is because, similarly to the kmeans clustering and as we will see below, these clusters include only Nevada and Washington DC, respectively.

mclust_fit_eii$parameters$variance$Sigma[1,1]
mclust_fit_eii$parameters$variance$Sigma[2,2]
mclust_fit_eii$parameters$variance$Sigma[1,0]

## [1] 0.8824481
## [1] 0.8824481
## numeric(0)

mclust_fit_eei$parameters$variance$Sigma[1,1]
mclust_fit_eei$parameters$variance$Sigma[2,2]
mclust_fit_eei$parameters$variance$Sigma[1,0]

## [1] 0.8499357
## [1] 1.36767
## numeric(0)

These variances and covariance illustrate the modelling assumptions made here. For EII, the variance is the same for both indicators 1 and 2 (and for all other indicators), whereas it differs for for the EEI model, where we allowed the clusters to be narrower/wider with respect to different indicators.

However, as both of these models do not allow for correlation/variance between the indicators, the covariance between indicators 1 and 2 is 0 (as are all other covariances).

Note that we cannot fit Gaussian mixture models with correlation between indicators (so no ellipsoidal clusters) or with different standard deviations across clusters (so no unequal volume) to these data because there are not enough units (51) relative to the number of indicators (21), as shown below:

## any other model with either unequal volume, unequal shape or ellipsoidal clusters 
## won't work here because of the low number of units vs indicators
Mclust(bea,G=5,modelNames = "VII") # spherical, unequal volume, equal shape

## NULL

Mclust(bea,G=5,modelNames = "EVI") # diagonal, equal volume, varying shape

## NULL

Mclust(bea,G=5,modelNames = "EEE") # ellipsoidal, equal volume, equal shape

## NULL

9. Compare the cluster assignments from these two models ($classification in the saved model object) to those from the k-means clustering. You should be able to find two clusterings that exactly match. Explain why. Remember that the specific numerical labels (1, 2, 3, 4 and 5) are completely arbitrary, it is the groupings that are meaningful.

The easiest way to compare the clusters is to cross-tabulate them with the clusters from the k-means analysis. If you do this for various pairwise comparisons of clusterings, you will eventually find some that match. The clusters from the k-means on the unstandardised data exactly match those from the gaussian mixture model with spherical, equal volume clusters (EII):

# k-means vs EII clusters
table(kmeans_unstandardised$cluster, mclust_fit_eii$classification)

##    
##      1  2  3  4  5
##   1  0  0 18  0  0
##   2  0  0  0  0  1
##   3  8  0  0  0  0
##   4  0  0  0  1  0
##   5  0 23  0  0  0

The reason that these clusterings exactly match is the the Gaussian mixture model in which all indicators have the same variance (spherical) and all clusters are equal volume is functionally identical to a k-means clustering on the unstandardised indicators. Both models will treat variance in all indicators as equally important to explain, they are functionally the same clustering algorithm.

# k-means clustering vs EEI clusters
table(kmeans_unstandardised$cluster, mclust_fit_eei$classification)

##    
##      1  2  3  4  5
##   1  8  3  7  0  0
##   2  0  0  0  0  1
##   3  8  0  0  0  0
##   4  0  0  0  1  0
##   5  9 14  0  0  0

The EEI classification, however, gives slightly different cluster assignments that than the k-means clustering in two of the clusters.

10.2 Quiz

1. Which of the following is not true about Cluster Analysis?

1. All clustering methods seek to identify clusters of similar units. They differ in how they conceptualise the ‘similarity’.
2. Different methods may yield very different cluster distributions (size and shape).
3. The underlying algorithm is the same for all clustering methods.
4. The number/label that is given to a cluster by applying a clustering algorithm is generally entirely arbitrary.

2. K-means clustering works by…

1. Having all observations starting in one cluster, and then ‘move up’ the hierarchy by recursively splitting the clusters.
2. Calculating the mahalanobis distance between observations, and then split them such that mahalanobis distance is minimised within and maximised between clusters.
3. Having all observations starting in a cluster of their own, and then ‘move down’ the hierarchy by recursively merging pairs of clusters.
   
4. Split the data in groups such that the sum of squared distances to the group mean is minimised within and maximised between groups.

3. Unlike Principle Component Analysis, k-means clustering…

1. Does not require the indicators to be on comparable scales.
2. Will not yield as many clusters as there are indicators (unless the researcher wants to).
3. Does not weigh each indicator equally.
4. Is a generative measurement method.

4. Which of the following defines generative measures?

1. It is when a measurement method assumes that changes in the target concept generate changes in the measure through a direct causal pathway.
2. It refers to cases where we use our substantive knowledge of and/or data about the relationship between concept and indicators to connect the two.
3. It is when we use theory to derive predictions (hypotheses) which we use to draw conclusions about observations.
4. It is when a measure discriminates between different levels of the concept, implying that concept is being defined by the measurement strategy.

5. Which of the following does not apply to Gaussian Mixture models?

1. It assumes that the observed data are the result of a mixture of latent classes that each have their own normal (=gaussian) distribution.
   
2. They are applicable when the latent variable is thought of as categorical and the indicators are categorical.
3. It is a probabilistic model.
4. Model fit will not automatically increase with the number of classes.
5. They are applicable when the latent variable is thought of as categorical and the indicators are continuous.

References

Bartholomew, David J, Fiona Steele, Jane Galbraith, and Irini Moustaki. 2008. Analysis of Multivariate Social Science Data. Chapman; Hall/CRC.

Everitt, Brian, and Torsten Hothorn. 2011. An Introduction to Applied Multivariate Analysis with r. Springer Science & Business Media.